
However, the names of higher-order hypercubes do not appear to be in common use for higher powers. A 9D hypercube would have 29 vertices, and each face would still use 4 vertices. As a result, the act of raising a number to 2 or 3 is more commonly referred to as " squaring" and "cubing", respectively. Proof: Each vertex has n edges incident to it, since there are exactly n bit positions. The same procedure works for the four-dimensional cube. Claim: The total number of edges in an n-dimensional hypercube is n2n1. Let f(n) denote the maximum number of edges in a subgraph of Qn con- taining no C4. Therefore the correct number of edges is 12, or three times half the number of vertices. following Ramsey theorems for hypercubes: A hypercube can always be. But this procedure counts each edge twice, once for each of its vertices. Similarly, the exponent 3 will yield a perfect cube, an integer which can be arranged into a cube shape with a side length of the base. At each vertex there are 3 edges, and since the cube has 8 vertices, we can multiply these numbers to give 24 edges in all. For example, the exponent 2 will yield a square number or "perfect square", which can be arranged into a square shape with a side length corresponding to that of the base. Generalized hypercubesĪny positive integer raised to another positive integer power will yield a third integer, with this third integer being a specific type of figurate number corresponding to an n-cube with a number of dimensions corresponding to the exponential. A unit hypercube's longest diagonal in n dimensions is equal to n. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. In geometry, a hypercube is an n-dimensional analogue of a square ( n = 2) and a cube ( n = 3).
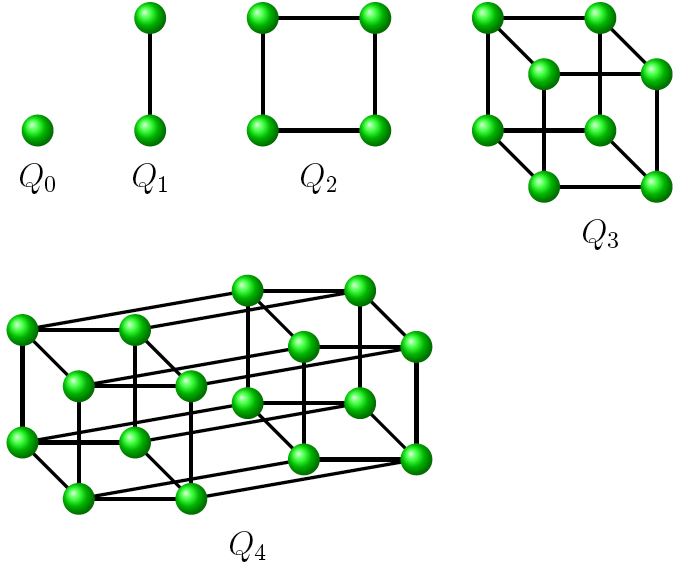
For the four-dimensional object known as "the" hypercube, see Tesseract. An edge is determined by the three coordinates that don't change.

How many edges An edge is two points that differ in only one place, such as ( 0, 0, 1, 0) and ( 0, 1, 1, 0). Thus there are 2 4 vertices (one for each quadruple). For internetwork topology, see Hypercube internetwork topology. Your hypercube is determined by the vertices ( 0, 0, 0, 0), ( 0, 0, 0, 1), ( 0, 0, 1, 0), ( 0, 0, 1, 1), etc. For the computer architecture, see Connection Machine. This article is about the mathematical concept. They also gather enough evidence to prove that is takes only 5 hyperplanes to cut all edges of a 5thdimensional hypercube, only 5 hyperplanes to cut all edges of a 6thdimensional hypercube, and 5 or 6 hyperplanes to cut all edges of a 7thdimensional hypercube.


 0 kommentar(er)
0 kommentar(er)
